Holographic signatures of resolved cosmological singularities

After some longer silence partly due to moving to a new location (LMU Munich) and teaching my first regular lecture (Theoretical mechanics for lyceum teachers and computational science at Regensburg University), I hope to write more regularly again in the future.

As a start, a new paper on using loop quantum gravity in the context of AdS/CFT has finally appeared here. Together with Andreas Schäfer and John Schliemann from Regensburg University, we asked the question of what happens in the dual CFT if you assume that the singularity on the gravity side is resolved in a manner inspired by results from loop quantum gravity.

Building (specifically) on recent work by Engelhardt, Hertog, and Horowitz (as well as many others before them) using classical gravity, we found that a finite distance pole in the two-point-correlator of the dual CFT gets resolved if you resolve the singularity in the gravity theory. Several caveats apply to this computation, which are detailed in the papers. We view this result therefore as a proof of principle that such computations are possible, as opposed to some definite statement of how exactly they should be done.

Coarse graining and state refinements

Coarse graining has become an increasingly important topic in loop quantum gravity with several researchers working on it. As usual in physics, one is interested in integrating out microscopic degrees of freedom and doing computations on an effective coarse level. How exactly the states, observables, and dynamics of the theory should change under such a renormalisation group flow is only poorly understood at the moment.

Recently, I have written a paper about this topic in a simplified context which is tailored to reproduce loop quantum cosmology from loop quantum gravity. Here, one can explicitly coarse grain the relevant observables, the scalar field momentum and the volume of the spatial slice, and check that their dynamics remains unchanged under such a coarse graining.

The reason that this works is rooted in an exact solution to loop quantum cosmology which can be imported in this full theory setting. In particular, the form of the dynamics of this solution is independent of the volume of the universe. It then follows that if we concentrate the volume of some set of vertices at a single one, the evolution of this coarse grained volume will agree with the evolution of the sum of the individual volumes.

The content of the paper is sketched in the brief talk linked above.

Heuristics for Lorentz violations in LQG

Slight energy dependences in the speed of light can accumulate over time,
allowing for possible detection or exclusion of such effects. Highly energetic
photons emitted e.g. by a supernova are in particularly useful for such studies.

Predictions for possible Lorentz violations are a key area of interesting phenomenology in quantum gravity. Within loop quantum gravity, it has not been possible so far to reliably extract predictions for Lorentz violations. Existing claims were based on simplified toy models inspired by LQG, but not implied. This situation hasn’t changed so far, but there is an interesting development which hints at which order we might expect such Lorentz violations to be found.

Elements of loop quantum gravity

After some longer silence on this blog, I am happy to announce that the introductory lectures from which excerpts have appeared here before are finally online.

The lectures start with a general introduction to quantum gravity, including a theoretical motivation, possible experimental tests, and the previously posted list on approaches to the subject. There is also an improved (as compared to here) estimate on the local Lorentz invariance violation based on anomaly freedom of effective constraints. I am planning to write about it in more detail in the future.

Next, an introduction to loop quantum cosmology is given, a draft of which has appeared here before. The new version features some improvements in the presentation and some simplifications in the derivation.

The remaining part of the lectures introduces full loop quantum gravity with minimal technical details. The derivation of geometric operators is sketched and different approaches to the dynamics are discussed. Promising lines of current research are mentioned and evaluated. Exercises are included at the end of each section.

The present lecture notes are somewhat complementary to several other sets of lecture notes existing in the literature in that they refrain from technical details and give a broad overview of the subject, including motivations and current trends. If someone spots mistakes or has suggestions for a better presentation, I would be happy to hear about it.

Strings meet Loops via AdS/CFT (Helsinki Workshop on Quantum Gravity 2016)

This rerecorded talk was originally given at the Helsinki Workshop on Quantum Gravity on June 2, 2016. I was invited by the organisers to talk about a recent paper, which was intended as an invitation for people to become interested in the subject, as opposed to giving concrete and detailed results.

In particular, I am very much looking forward to discussions about this topic and criticism of the ideas, in particular from experts in string theory. In the long run, much can be gained in my point of view from intensifying the exchange between researchers in loop quantum gravity and string theory.

In this context, it is certainly worth pointing out a recent article by Sabine Hossenfelder for Quanta Magazine, as well as a blogpost of hers on the paper I wrote.

Graph superspositions and improved regularisations

In loop quantum gravity, the elements of a certain basis in the Hilbert space
can be (roughly) interpreted as lattices. Generic quantum states can be constructed
as superpositions thereof and a priori have different properties which cannot
be realised at the level of individual lattices. 

Let us pick up the topic of extracting effective cosmological dynamics from loop quantum gravity again. Today’s post is about a recent paper by Emanuele Alesci and Francesco Cianfrani within their framework of “Quantum reduced loop gravity”. This version of loop quantum gravity is arrived at by a gauge fixing to the diagonal metric gauge at the quantum level (as opposed to the classical level as e.g. here), along with a truncation of the Hamiltonian constraint consistent with a spatially homogeneous setting (in particular, the non-trivial shift resulting from the gauge fixing is dropped). The simplified quantum dynamics resulting form this gauge fixing have allowed to compute the expectation value of the Hamiltonian constraint in suitable coherent states, leading to the effective Hamiltonian that one finds in loop quantum cosmology.

An open issue in this context has been to properly derive the so called “improved “ dynamics of loop quantum cosmology, which are consistent with observation and do not feature some unphysical properties of the original formulation. This is somewhat tricky if one uses standard connection variables along with a gauge group like SU(2) or U(1) for the following reason:

Progress on low spins

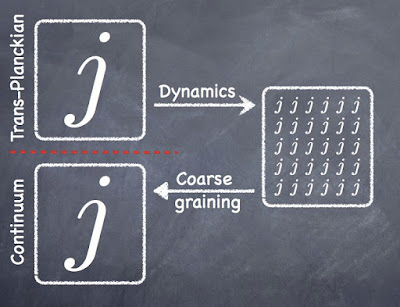Fundamental (trans-Planckian) large spins are expected to decay into
many small spins under the dynamics. An explicit calculation showing
  this has been given now within group field theory. At the same time,
one can coarse grain the many small spins into few large spins to have
an effective continuum description. The precise relation between those
two, a priori distinct large spin regimes is so far unclear.  

The fundamentally important issue of low and high spins in the dynamics of LQG has been discussed in previous posts. In short, large geometries can be described using either many low or few large quantum numbers (SU(2) spins), but the respective dynamics needs to be interpreted with care. In particular, using large spins to describe continuum geometries requires to understand the renormalisation group flow of the theory. Most work in LQG has so far been in the context of large spins (without considering renormalisation), where calculations simplify drastically due to the availability certain asymptotic formulae for the SU(2) recouping coefficients with nice geometric interpretations. However, there seems to be some progress now on the low spin front. 

Is loop quantum gravity based on discretisations?

Two spin networks, which can be interpreted as Hilbert space elements
describing truncations (or discretisations) of general relativity,
are summed. What is the physics of such states? 

This post is related to last week’s about criticism of loop quantum gravity and a comment I found in Sabine Hossenfelder’s blog. Saying that loop quantum gravity is based on discretisations quickly leads one to doubt that Lorentz invariance may be a property of LQG, as happened in the comment. So it seems worth to clear up this issue and precisely say in what context discretisations appear, in what context they don’t, and what this means for the physics that are described by LQG.

Updates on some criticisms of loop quantum gravity

Image from MySafetySign.com

In this post, we will gather some criticism which has been expressed towards loop quantum gravity and comment on the current status of the respective issues. The points raised here are the ones most serious in my own opinion, and different lists and assessments could be expressed by other researchers. 

Approaches to quantum gravity

Again as a part of a lecture series in preparation, I compiled a list of the currently largest existing research programmes aimed at finding a quantum theory of gravity (while unfortunately omitting some smaller, yet very interesting, approaches). A much more extensive account is given in here. For an historical overview, I recommend this paper.

How does loop quantum cosmology work?

The evolution of the expectation value of the volume v of the universe is plotted.
The blue and orange lines are the expanding and contracting branches in the
Wheeler-de Witt theory. The green curve follows from loop quantum cosmology
and exhibits a quantum bounce close to Planck density.

These days I have been working on lecture notes for an introductory lecture series on loop quantum gravity. An introductory article by Abhay Ashtekar introduced this subject via a discussion on loop quantum cosmology (LQC), where already many of the essential features of loop quantum gravity are present and can be studied in a simplified setting. I think that this is a very useful pedagogical approach and I also wanted to incorporate it into my lectures. I just finished my first draft of a lecture about this subject, focussing on a specific exactly soluble LQC model and its comparison to a similar quantisation using the Wheeler-de Witt framework. Mostly I follow the original paper, with some additional comments, slight rearrangements, and omission of more advanced material that is not necessary in an introductory course in my point of view. The current draft is available here, and comments are always welcome.

The short version goes as follows:

Yang-Mills analogues of the ambiguities in defining LQG geometric operators

Changing the connection variables underlying loop quantum gravity
also changes the geometric operators. They measure geometry with respect
to the metric encoded in the Yang-Mills electric field $E^a_i$.   

tl;dr: In some cases there are such analogues, but they are rather awkward.

A comment to a recent post on the current status of the issue of the spectra of geometric operators in loop quantum gravity raised the question of whether such ambiguities can also be found in Yang-Mills theory. The question if of course very interesting, however I am not aware of any reference commenting on it. So let me try.

Some comments on the properties of observable algebras

An example of non-locality in an observable algebra. Observables are
defined as fields at the endpoints of geodesics. Changing the metric
along the geodesic via $P^{rA}$, the field conjugate to some of the relevant
components of the spatial metric, leads to an apparent non-locality due to
a rerouting of the geodesic.

A recent post contained a talk of mine of a specific construction of observables in general relativity, where a physical coordinate system was specified by the endpoints of certain geodesics. The so constructed coordinates are simply Gaußian normal coordinates and the usual relational construction of observables as fields at a physical point could proceed in the standard manner.

The motivation for the underlying paper came from AdS/CFT, where people were interested in constructing CFT operators corresponding to scalar fields in the bulk, localised at the endpoint of a geodesic. While the scalar fields were argued to commute in this construction, a contradictory statement was recently made in a perturbative calculation. To settle this question, we upgraded a calculation referring to spatial geodesics, based on this seminal work, to the case of spacetime geodesics considered in the AdS/CFT case.

The calculation which we performed illustrates nicely some points about the properties of observables which are often not spelled out, however seem of relevance for researchers interested in quantum gravity and should not be confused. In this post, we will gloss over global problems in defining observables, see e.g. this paper and references therein for a recent interesting discussion. See also this post for an earlier discussion of observables and the control we have on them.


1. Structure of the (sub-)algebra of observables
When we quantise, we always pick some preferred subalgebra of phase space functions that we want to quantise. It is well known that we cannot quantise all functions at the same time, as formalised in the Groenewold-van Hove theorem. Therefore, also in canonical quantum gravity such a choice has to be made, independently of whether we first quantise or first solve the constraints. We are interested here in the latter case, i.e. in the quantisation of a complete (= point separating on the reduced phase space) set of Dirac observables, or equivalently a complete set of phase space functions after gauge fixing the Hamiltonian and spatial diffeomorphism constraints, although similar statements should in principle also hold in the former case.
The precise nature of this choice will determine the properties of our observable algebra. In particular, examples can be given where

1. the resulting algebra has a perfectly local structure (e.g. when employing dust to specify a reference frame),
2. the resulting algebra is local, but some phase space functions not contained in the complete sub-algebra have non-local commutation relations
3. the resulting algebra is non-local

Roughly, the following happens. If we localise some field with respect to some locally defined structure, such as the values that four scalar fields take at a point, then the algebra remains local, where local means that Poisson brackets will be proportional to a delta-distribution in the coordinates defined by the scalar field coordinates. Another such example is to use dust. We can however also localise some field with respect to a more global structure, such as the endpoint of a spatial geodesic originating from some observer or the boundary of the spatial slice. Then, phase space functions with a non-vanishing Poisson bracket with components of the metric specifying this geodesic will have non-local (in the coordinates specified by the geodesics) Poisson brackets with fields localised at the endpoints of geodesics, just because they change the geodesic which defines the point where the field is evaluated. However, it is still possible to pick a complete set of such observables which have local Poisson brackets among themselves if we pay attention not to include fields not commuting with the components of the metric determining the path of the geodesics. This is in fact what is happening here. For the last case, we simply locate our fields with respect to some extended structure that is specified using non-commuting phase space functions, e.g. a spacetime geodesic. This doesn’t mean that locality breaks down, it simply means that we are considering observables which are smeared over regions of spacetime, and two such regions associated to different localisation points might overlap.


2. Locality of the physical Hamiltonian
Another question is whether the physical Hamiltonian that one derives with respect to a certain choice of time will be non-local. Again, in the case of dust as a reference field, it is local. However, already in the second case above one finds that is non-local, simply because it contains the phase space functions which have non-local Poisson brackets. Since a generic Hamiltonian will contain all fields of the theory, it seems that one has to avoid relational observables with respect to non-local structures if one wants to obtain a local Hamiltonian. However, it should be stressed again that one still might have a complete local observable algebra, even though the Hamiltonian is non-local. A detailed example is given here.


3. Independence of spacetime boundaries
All arguments made above are independent of the structure of the spacetime at infinity. In particular, the math involved in constructing observables and computing their algebra, see e.g. here, here, and here, does not refer to infinity. Also, the fact that the on-shell Hamiltonian constraint is a boundary term is not of relevance here, as it generates evolution via its Hamiltonian vector field, which is non-vanishing on-shell. Once a clock field is chosen on the other hand, one obtains a physical Hamiltonian with respect to that clock which is non-vanishing on-shell. Therefore, as long as one can locally define a clock, one can also have evolution. 

The algebra of observables in Gaußian normal space-(time) coordinates

This rerecorded talk was originally given at the spring meeting of the German Physical Society on February 29, 2016. It is based on this paper, where the algebra of a set of gravity observables constructed using a coordinate system specified by geodesics is computed. My interest in this question, next to general considerations in quantum gravity, comes from the AdS/CFT correspondence, where this construction has been used in the construction of the bulk / boundary dictionary. I plan to comment a little more on the content of the paper in the near future, highlighting some in my point of view important conceptual conclusions on the structure of general relativistic observable algebras.

Are the spectra of the LQG geometric operators really discrete?

tl;dr: Sometimes yes, sometimes no, depending on how one passes to the physical Hilbert space.

The title for this post is shamelessly borrowed from this paper, where Bianca Dittrich and Thomas Thiemann have discussed this question some time ago, concluding that the answer could be negative at the level of the physical Hilbert space, i.e. after solving the Hamiltonian constraint. Carlo Rovelli then wrote a rebuttal, arguing that discreteness should remain also at the physical level. Since those papers, some time has passed and new light has been shed on this issue from various angles, to be reviewed in this post.

Helsinki Workshop on Quantum Gravity

http://www.visitfinland.com/helsinki/

From June 1-3, there will be a quantum gravity workshop in Helsinki, a kind of inaugural meeting for the field in Finnland. Mostly young people were invited to give talks, which should give a fresh view on the subject and hopefully result in collaboration across traditional subfield boundaries. I will talk about some recent ideas of connecting loop quantum gravity and string theory by using the gauge / gravity correspondence, with some comments already having appeared here.

On a related note, Sabine Hossenfelder has recently written a very nice article for quanta magazine about the possible connection between these subjects, based on interviews with several researchers in the field. Seeing that more people are becoming interested in this subject is certainly a great encouragement in further pursuing this direction.

Theta ambiguity, maximal symmetry, and the isolated horizon boundary condition

In a paper from last week, I discussed the relation between the three above concepts, which at first may seem unrelated. The bottom line is that there exists a 1-parameter family of vacua for LQG which seem to be largely unknown. The vacua are induced by the standard Ashtekar-Lewandowski functional, however the underlying holonomy-flux-algebra is based on connection variables where the densitised triad is shifted as $P^{ai} = E^{ai} + \theta \epsilon^{abc} F_{bc}^i$. This actually corresponds to a rigorous implementation of the so called Kodama state in the context of real variables. Since all fluxes annihilate the Ashtekar-Lewandowski vacuum, the condition $P^{ai}=0$ is implemented by the vacuum and equivalent to
\[q_{c[a} q_{b]d} = \beta \theta F_{abcd} = \beta \theta R^{(3)}_{ab cd} - 2 \beta^2 \theta \epsilon_{cde} \sqrt{q} \nabla_{[a} K_{b]} {}^e - 2 \beta^3 \theta K_{c[a} K_{b]d} \]
with $\beta$ being the Barbero-Immirzi parameter. In case of a vanishing extrinsic curvature $K_{ab}$, this condition is nothing else than maximal symmetry for the spatial geometry. A vacuum based on variables with $\theta \neq 0$ is thus very interesting from the point of view of constructing semi-classical states, since it is peaked on a non-degenerate homogeneous geometry. $0 < \theta < \infty$ thus seems to interpolate between the Ashtekar-Lewandowski vacuum ($\theta=0$) and the recently introduced Dittrich-Geiller vacuum, which implements $F = 0$.

People familiar with isolated horizons and their application in LQG will also notice the strong similarity of the condition $P^{ai}=0$ with the isolated horizon boundary condition which is imposed in the black hole entropy computation in LQG (a pullback of $P^{ai} = 0$ to a 2-surface with $\theta$ depending on the total black hole area). It was shown before that computations along the original lines are actually applicable to general boundaries. Here, we also see that trying to impose the isolated horizon boundary condition directly on the full LQG Hilbert space is only enforcing a part of maximal symmetry condition, as opposed to selecting horizons (in contrast to what is often suggested). Thus, also less mainstream works along these lines, while very interesting, do not provide suitable definitions of quantum horizons, but rather quantum symmetric surfaces.

What does it mean to derive LQC from LQG?

Recently, I have been thinking about the question what it actually means to derive loop quantum cosmology from loop quantum gravity. In other words, what is the benchmark by which we can claim success in this task? Given that several interesting proposals for such a derivation have appeared recently, it is time to ask this meta-question.

First, one should probably ask two different questions as a warm up:

1) What is the cosmological sector of LQG?

2) What is LQC?

An example of a good talk

A few days ago, I collected some general recommendations for preparing good slides. Shortly before I started to look into these ideas, I saw an example of a, in my point of view, very good talk, which incorporated many of the points I mentioned. Since examples are usually very helpful in grasping some new idea, I decided to explain why I think that this talk was so well done.

The talk I am referring to was given by Jędrzej Świeżewski from the University of Warsaw in the International Loop Quantum Gravity Seminar. Here are direct links to the slides and audio.

How to give a good talk and avoid common mistakes

Recently, I became aware of a large amount of literature and tutorials online about how to prepare proper slides for talks. While I was paying attention on certain aspects of my slides previously, it occurred to me that there were still many crucial problems in the slides I prepared so far, which must have unnecessarily hindered people in following what I was trying to say. My two ILQGS talks from 2013 and 2015 serve as a good example of the different approach to preparing slides, the 2015 one was my first talk prepared taking into account some of the points that I will discuss below.

Anti de Sitter spaces from finite Spin Networks

This video is my first example of a “short talk”, a presentation intended to quickly outline the main idea of a paper while skipping as much technicalities as possible. The interested reader can then consult the paper for more details.

This option seems more useful to me than trying to press too many technicalities in a talk, especially given that nowadays it is practically impossible to follow all interesting developments at a reasonable technical level.

I hope to generate more of these short presentations in the future, also taking into account some of my older papers.

I heard of this idea originally in some invitation to provide such a presentation for the PLB homepage, were it is implemented as a system called “AudioSlides”.

Late registration for Tux 2016

There are still a few places left for this year's Tux workshop on quantum gravity, February 15-19, including talk spots. If you are interested, please follow the instructions at the conference webpage.

Quantum Theory and Gravitation @ DPG Spring Meeting 2016 in Hamburg

This years spring meeting of the German Physical Society (DPG) will feature a symposium about quantum theory and gravitation. Plenary speakers include Abhay Ashtekar, Gerard 't Hooft, Markus Aspelmeyer, Hermann Nicolai, Renate Loll, and Christian Wüthrich.

The conference will take place from 29.02.-04.03.2026, however the symposium talks are planned for Tuesday and Wednesday of that week. In addition, there will be regular contributed talks.

For more (or currently less) information, see the conference homepage.

Black hole entropy from loop quantum gravity: Generalized theories and higher dimensions (ILQGS)

Talk given at the International Loop Quantum Gravity Seminar (ILQGS) on October 1, 2013.

Slides (PDF) are available at: http://relativity.phys.lsu.edu/ilqgs/

Based on the original research papers
http://arxiv.org/abs/1304.2679
http://arxiv.org/abs/1304.3025
http://arxiv.org/abs/1307.5029

Addendum:
- More discussion on the quantisation and the relation to entanglement entropy is discussed in http://arxiv.org/abs/1402.1038

Symmetry reductions in loop quantum gravity based on classical gauge fixings (ILQGS)

Talk given at the International Loop Quantum Gravity Seminar (ILQGS) on December 8, 2015.

Slides (PDF) are available at: http://relativity.phys.lsu.edu/ilqgs/

Based on the original research papers
http://arxiv.org/abs/1410.5608
http://arxiv.org/abs/1410.5609
http://arxiv.org/abs/1512.00221
http://arxiv.org/abs/1512.00713

Addendum:
- On slide 10, an additional reference to http://arxiv.org/abs/gr-qc/0211012 should be added.

Do we really not have observables for GR?

One often hears or reads that we do not have observables for GR, except maybe for the ADM charges. For interpreting the theory, this sounds like a serious obstacle. However, the situation is by far not as bad as one might naively conclude form this statement, and conceptually in fact rather clear.