Progress on low spins

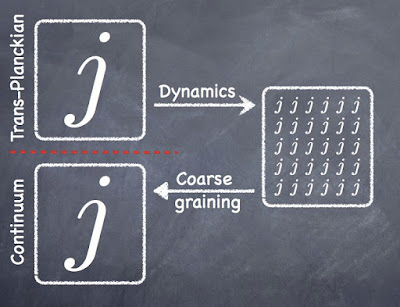
Fundamental (trans-Planckian) large spins are expected to decay into
many small spins under the dynamics. An explicit calculation showing
  this has been given now within group field theory. At the same time,
one can coarse grain the many small spins into few large spins to have
an effective continuum description. The precise relation between those
two, a priori distinct large spin regimes is so far unclear.  

The fundamentally important issue of low and high spins in the dynamics of LQG has been discussed in previous posts. In short, large geometries can be described using either many low or few large quantum numbers (SU(2) spins), but the respective dynamics needs to be interpreted with care. In particular, using large spins to describe continuum geometries requires to understand the renormalisation group flow of the theory. Most work in LQG has so far been in the context of large spins (without considering renormalisation), where calculations simplify drastically due to the availability certain asymptotic formulae for the SU(2) recouping coefficients with nice geometric interpretations. However, there seems to be some progress now on the low spin front. 

Last month, Steffen Gielen showed in a paper that a low spin regime dynamically emerges within the group field theory framework. Group field theory (GFT) is a quantum field theory defined on a group manifold and constitutes a quantum field theory of spacetime (as opposed to a quantum field theory on spacetime). Its basic excitations above the “no space” Fock vacuum are the quanta of geometry that one also considers in loop quantum gravity. In fact, spin foam amplitudes can be obtained from the perturbative expansion of group field theories, linking it to the path integral formulation of loop quantum gravity. 

More precisely, Steffen showed that the group field theory dynamics, in a suitable approximation and for the simplest choice of kinetic term, exponentially suppress all but the lowest spins. The work has been in the context of deriving loop quantum cosmology from loop quantum gravity and thus naturally relies on some assumptions. A weak coupling limit is used, where the interaction term in the group field theory Lagrangian is neglected. The kinetic term is taken to be a a constant plus the Laplacian on the group (which is well motivated by GFT renormalisation) as well as for a coupled massless scalar field. The dynamics are computed in a hydrodynamic limit using the Gross-Pitaevskii equation. The wave function is taken to be the simplest possible condensate state and the tetrahedra are restricted to be equilateral. Then, for a certain choice of coupling parameters in the group field theory action, the above result follows. For other parameters, no semiclassical geometry seems to emerge. In addition, one has to exclude vanishing spins $j=0$ by hand (which is dynamically stable), as these play a little different role in GFT than in standard LQG. 

The calculation is then extended to a more general class of models previously considered here and here by Daniele Oriti, Lorenzo Sindoni, and Edward Wilson-Ewing. By adjusting additional parameters, the dominating spin can be set to some value $j_0$. The case $j_0 = 1/2$ obtained already in the simplest case is however favoured by naturalness and also enters the (heuristic) derivation of the Hamiltonian constraint in loop quantum cosmology. In any case, these models then agree with the Friedmann dynamics for large volumes of the universe. The effective dynamics of loop quantum cosmology is obtained up to a correction term which is suppressed by the volume of the universe in Planck units. In particular, higher spins are excited in the Planck regime, which is not taken into account in LQC and thus constitutes a genuine full theory correction to the mini-superspace quantisation in LQC. 

Even despite these assumptions, the result is very interesting and seems for the first time to demonstrate that a low spin regime dynamically emerges from loop quantum gravity, or, more precisely, the group field theory approach to it. This result then underlines the importance of studying the effective dynamics of large spin descriptions of continuum geometries via a renormalisation group analysis starting at the lowest possible spins. Otherwise, a transplanckian interpretation of the large spin regime seems more appropriate. 

Previous results where low spins were dominant were computations of black hole entropy. However, these computations are by construction insensitive to the quantum dynamics.